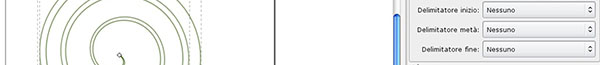Dopo aver appreso nella precedente lezione come disegnare oggetti bidimensionali di base, passiamo ora alle forme complesse in Inkscape: analizzeremo il funzionamento degli strumenti Stelle e Poligoni, quindi delle Spirali.
Stelle e Poligoni
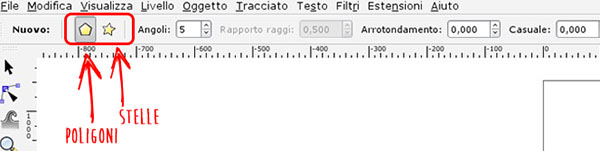
Selezionando lo strumento Stelle e Poligoni, abbiamo a disposizione la scelta di quale dei due tool utilizzare direttamente nella barra Impostazione Strumenti, come illustrato in Figura 1.
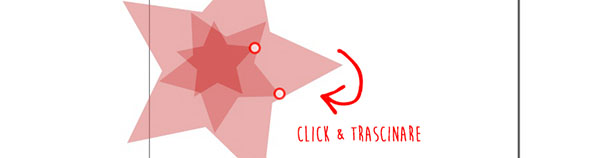
Selezioniamo lo strumento a forma di stella e proviamo a disegnare sul foglio, cliccando con il mouse e trascinando fino a che dimensione e orientamento ci soddisfano. Finché non rilasciamo la pressione sul tasto del mouse, possiamo continuare a modificare la forma della stella che stiamo disegnando, come mostrato in Figura 2.
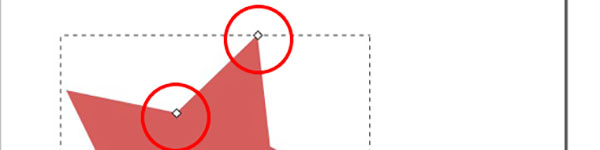
Rimanendo sullo strumento Stelle e Poligoni notiamo che, come negli esempi della lezione precedente, sulla figura sono apparsi due indicatori, ovvero delle maniglie
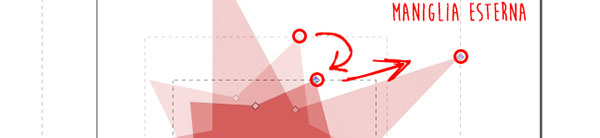
Come ormai sappiamo, agendo sulle maniglie di un oggetto possiamo modificarne la forma. Vediamo in dettaglio come si comporta la funzione sull'oggetto stella. Se trasciniamo la maniglia esterna spigolosità poligono
Vediamo ora cosa succede quando andiamo a selezionare la maniglia interna
L'ultima opzione legata alla stella è quella che interviene sull'arrotondamento degli angoli Impostazione Strumenti
Spirali
Per creare una forma a spirale, selezioniamo lo strumento corrispondente dal pannello e disegniamo l'oggetto sul foglio. Le caratteristiche della forma possono essere modificate dal pannello Impostazione Comandi. Da qui si possono modificare il tratteggio, lo spessore della linea, il colore e molto altro, come dimostrato in Figura 7.
Caratteristica degli oggetti ormai consolidata, anche per questa forma abbiamo modo di agire sulla spirale trascinando le maniglie: in questo caso la trasformazione aumenterà o diminuirà il numero di rotazioni
Per cambiamenti più specifici alla forma dobbiamo rivolgere l'attenzione alla barra Impostazioni Strumenti. Come possiamo vedere, sono a nostra disposizione tre campi: Rivoluzioni Divergenza Raggio Interno
Invece, modificando la divergenza andremo ad allargare o restringere la distanza tra un giro di spirale e quello seguente, come evidente in Figura 10.
Il raggio interno dilata o restringe l'angolo di curvatura, trasformando così l'arco della spirale, come infine illustrato in Figura 11.
