A questo punto dobbiamo spiegare meglio come riuscire a formalizzare in maniera logica i concetti che vogliamo trasformare in programma; questa operazione è forse la più importante e complessa, perché è su questa che poi si baserà il lavoro di scrittura del codice che andremo a mettere in atto.
I due strumenti che ci vengono in soccorso sono l'Algebra di Boole (utile per le operazioni sui dati) ed i diagrammi di flusso (utili per rappresentare in maniera ordinata i nostri processi logici).
L'Algebra di Boole come base per la programmazione (e non solo)
Apriamo una piccola parentesi sull'Algebra di Boole; questo tipo di logica non è correlata esclusivamente al mondo della programmazione, ma fa parte della vita di tutti i giorni. Pensiamo ad esempio a quando vogliamo uscire di casa, se piove non possiamo uscire; questo processo mentale, cioè il verificare se piove, può assumere, di fatto, due stati, o è vero (e quindi non usciamo) o è falso (e quindi usciamo). Si può capire che se questo tipo di logica risulta utile a noi come esseri umani, lo è ancora di più per un computer poiché il suo linguaggio è fatto solo di bit ed è possibile associare al vero il valore 1 ed al falso il valore 0.
L'Algebra di Boole verrà qui solamente accennata e sostanzialmente consiste nel prendere come valori "vero" e "falso" (o 1 e 0); posti questi valori andiamo a vedere come operazioni logiche producano dei risultati nuovi e sensati.
AND - Congiunzione
|
falso AND falso
|
risultato falso
|
|
falso AND vero
|
risultato falso
|
|
vero AND falso
|
risultato falso
|
|
vero AND vero
|
risultato vero
|
Riusciamo facilmente a comprendere che l'AND restituisce un valore vero "se e solamente se gli altri due valori sono veri", questo vuol dire che anche in una successione di più operazioni AND basta che un valore sia falso ed anche il risultato lo sarà.
OR - Disgiunzione
|
falso OR falso
|
risultato falso
|
|
falso OR vero
|
risultato vero
|
|
vero OR falso
|
risultato vero
|
|
vero OR vero
|
risultato vero
|
L'OR invece restituisce un valore vero "se e solamente se almeno uno dei due valori risulta vero"; in poche parole anche in una successione di più operazioni OR basta che un valore sia vero ed anche il risultato lo sarà.
NOT - Negazione
|
NOT falso
|
risultato vero
|
|
NOT vero
|
risultato falso
|
Il NOT si riduce ad una semplice operazione di negazione del valore acquisito.
Si può evincere che grazie all'Algebra di Boole è possibile formalizzare i nostri pensieri riuscendo così a creare strutture complesse di rapido utilizzo, ma che non erano direttamente connesse ai dati iniziali. Basti pensare che i microprocessori stessi si basano sulla semplice logica dell'Algebra di Boole, con la quale è possibile formalizzare qualsiasi tipo di ingresso.
I diagrammi di flusso
I diagrammi di flusso sono dei disegni che rappresentano graficamente un nostro ragionamento rappresentandolo come algoritmo, permettendo così, primo, una comprensione immediata del funzionamento del nostro percorso logico, secondo, un controllo accurato sulla funzionalità e la casistica del ragionamento.
Prima di procedere con un esempio pratico occorre definire i "simboli" utilizzati all'interno dei diagrammi di flusso per identificare i vari tipi di azione. Ci viene qui in soccorso la tabella sottostante che mostra i simboli ed il relativo significato per schematizzare il flusso del nostro ragionamento.

Si può facilmente capire che la schematizzazione di un algoritmo risulta quindi molto semplice, visto che ogni simbolo viene assegnato ad una fase del percorso logico che facciamo. Prendiamo in esame un semplice ragionamento che verifica se è possibile fare uno spuntino, tale programma viene spiegato come segue:
- Inizia lo spuntino
- Hai a disposizione qualcosa da mangiare?
- Mangia
- Hai ancora fame?
- Fine dello spuntino
Esposto in questo modo l'algoritmo risulta di difficile comprensione, ma rappresentandolo con un diagramma di flusso possiamo comprendere l'esatto funzionamento del ragionamento.
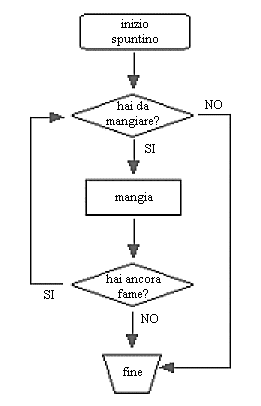
Naturalmente la teoria dei diagrammi di flusso risulta essere più complessa rispetto all'esempio sopraesposto, ma i dati forniti servono comunque per farsi un'idea di come uno strumento apparentemente semplice, possa essere usato per formalizzare anche concetti di grande entità e complessità.